Minimax Algorithm – Explained Using a Tit-Tac-Toe Game
A minimax algorithm is a recursive program written to find the best gameplay that minimizes any tendency to lose a game while maximizing any opportunity to win the game.
Graphically, we can represent minimax as an exploration of a game tree’s nodes to discover the best game move to make.
In such representation, the tree’s root node is the game’s current state—where the minimax algorithm got invoked.
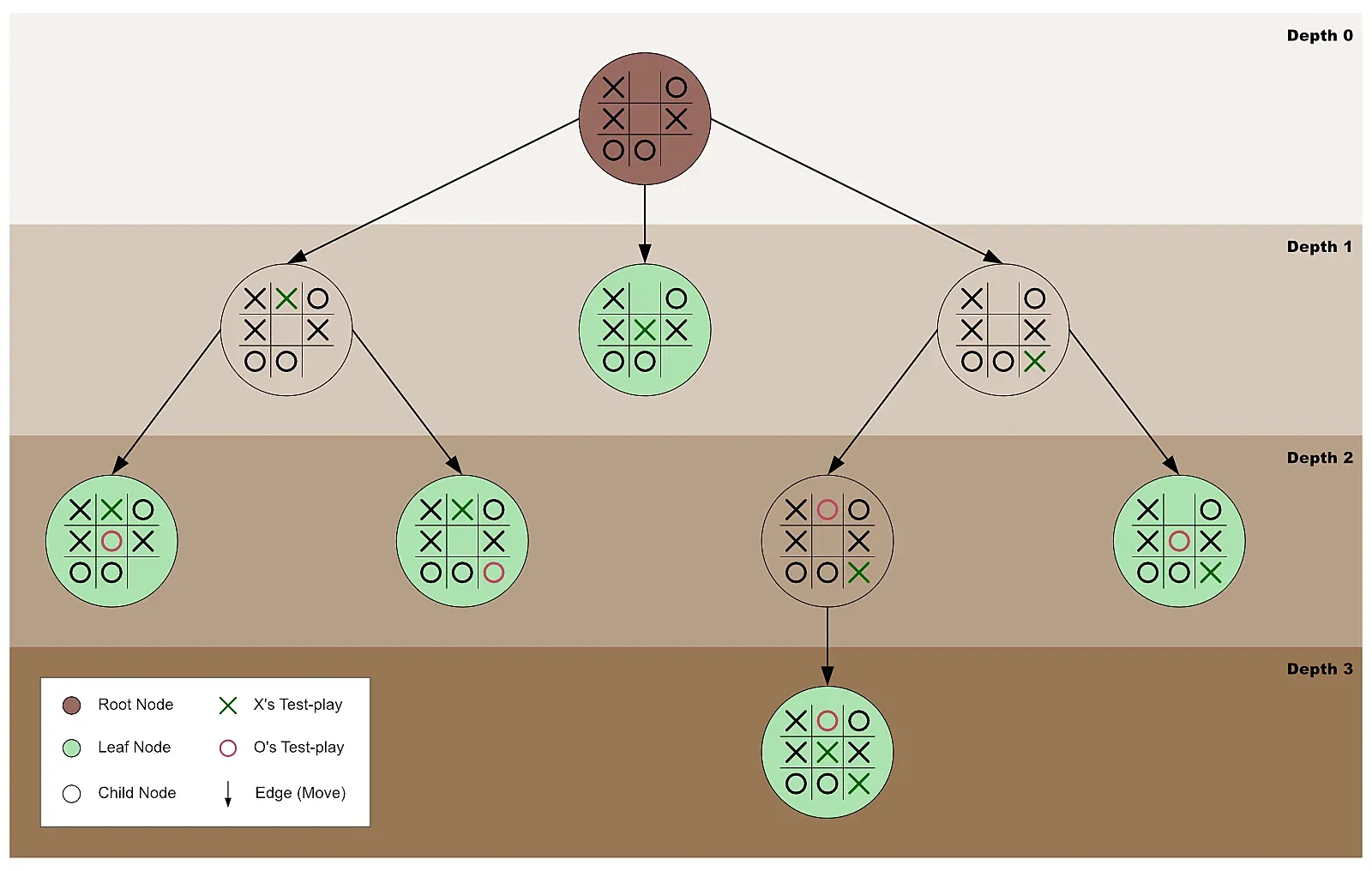
Figure 1: The game tree of a concluding tic-tac-toe game
Article’s Objective
Section titled “Article’s Objective”This article is a practical guide in which we will use a tic-tac-toe project to understand how minimax works.
The main goal of this article’s tic-tac-toe project is to create a minimax algorithm that makes the AI unbeatable.
Two standard terms you will often encounter in minimax algorithms are “maximizing player” and “minimizing player.” But what exactly do these terms mean? Let’s find out below.
Maximizing vs. Minimizing Player – What’s the Difference?
Section titled “Maximizing vs. Minimizing Player – What’s the Difference?”In most cases, the maximizing player is the player that initially invoked minimax. In other words, the original invocator of minimax is the player that wants to maximize any opportunity to win the game.
However, the minimizing player is the maximizing player’s opponent.
The minimizing player is the player whose chances of winning must be minimized.
Therefore, you could alternatively define the minimax algorithm as a recursive function created to help a player (the maximizer) decide on the gameplay that minimizes the maximum possibility of losing a game.
So, now that you know what “maximizing player” and “minimizing player” imply, let’s begin the process of making the AI unbeatable in a tic-tac-toe game!
Step 1: Get Familiar with This Tutorial’s Root Node
Section titled “Step 1: Get Familiar with This Tutorial’s Root Node”To make this tutorial precise, the root node (the current state of the tic-tac-toe game) we will use will be a near-the-end state game board—as shown in figure 2 below.
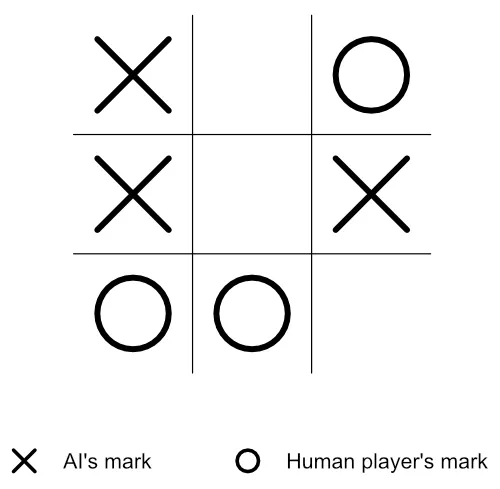
Therefore, open your editor, and let’s recreate this tutorial’s root node.
Step 2: How to Recreate This Tutorial’s Root Node
Section titled “Step 2: How to Recreate This Tutorial’s Root Node”The following sections will show you how to create the current state of the tic-tac-toe game, as illustrated in figure 2.
1. Create a project directory
Section titled “1. Create a project directory”Create a project folder—where this project’s HTML, CSS, and JavaScript files would reside.
2. Create your code files
Section titled “2. Create your code files”Create the following files inside your project folder.
index.htmlstyles.cssscript.js
3. Create the gameboard
Section titled “3. Create the gameboard”Open your index.html file and replicate the code below:
<!DOCTYPE html><html> <head> <meta charset="UTF-8" /> <meta name="viewport" content="width=device-width, initial-scale=1.0" /> <link href="https://fonts.googleapis.com/css2?family=Permanent+Marker&display=swap" rel="stylesheet" /> <link href="styles.css" rel="stylesheet" /> <title>Tic Tac Toe Game - CodeSweetly</title> </head> <body> <div id="tic-tac-toe-grid"> <span class="cell r1 c1 d1 h">X</span> <span class="cell r1 c2 h v"></span> <span class="cell r1 c3 d2 h v">O</span> <span class="cell r2 c1 h">X</span> <span class="cell r2 c2 d1 d2 h v"></span> <span class="cell r2 c3 h v">X</span> <span class="cell r3 c1 d2">O</span> <span class="cell r3 c2 v">O</span> <span class="cell r3 c3 d1 v"></span> </div> <button id="play-game-btn">Play Game</button> <button id="new-game-btn">New Game</button> <script src="script.js"></script> </body></html>Here are the main things we did in the HTML snippet above:
- We nested nine (9)
<span>elements inside a<div>container. (The<span>s represent the gameboard’s cells, while the<div>is the board.) - We created two
<button>elements.
4. Style the cells and board
Section titled “4. Style the cells and board”Open your styles.css file and replicate the code below:
#tic-tac-toe-grid { margin: 90px 0; display: grid; grid-template-columns: repeat(3, 130px); grid-template-rows: repeat(3, 130px); justify-content: center; text-align: center; font-size: 5.5rem; font-family: "Permanent Marker", cursive; color: #4b3621; touch-action: none; user-select: none;}
.cell { line-height: 130px;}
.h { border-bottom: 2.5px solid black;}
.v { border-left: 2.5px solid black;}
button { display: block; margin: 0 auto; padding: 7px 25px; border: 1px solid black; background: transparent; font-size: 1rem; cursor: pointer;}
#new-game-btn { display: none;}The CSS snippet above applied some styles to the gameboard, the cells, and the button elements.
5. Add some logic to your script file
Section titled “5. Add some logic to your script file”Open your script.js file and replicate the code below:
const playGameBtn = document.getElementById("play-game-btn");const newGameBtn = document.getElementById("new-game-btn");const gameCells = document.querySelectorAll(".cell");const aiMark = "X";const humanMark = "O";
let gameOver = true;
gameCells.forEach((c) => c.addEventListener("click", insertPlayersMark));playGameBtn.addEventListener("click", playGame);newGameBtn.addEventListener("click", startNewGame);
function insertPlayersMark() { if (!this.innerText && !gameOver) { this.innerText = humanMark; checkIfGameIsOver(); } if (!gameOver) { insertCompMark(); checkIfGameIsOver(); }}
function playGame() { insertCompMark(); checkIfGameIsOver(); playGameBtn.style.display = "none"; newGameBtn.style.display = "block";}
function startNewGame() { gameOver = false; gameCells.forEach((i) => { i.innerText = ""; i.style.color = "#4b3621"; });}
function insertCompMark() {}
function checkIfGameIsOver() {}In the JavaScript snippet above, we:
- Initialized three separate variables with the HTML document’s button elements and the gameboard’s cells.
- Assigned
"X"as the AI’s mark and"O"as the human player’s mark. - Initialized the
gameOvervariable with the Boolean valuetrue. - Added event listeners to the button elements and each cell of the gameboard.
6. View the gameboard
Section titled “6. View the gameboard”Open your index.html file in any browser to see the current state of your gameboard.
Once you’ve opened your HTML file, your gameboard should look as illustrated in figure 2. You can also see mine.
Keep in mind that the X mark represents the AI’s mark, while the O mark is the human player’s mark.
In the current stage of the tic-tac-toe game, it’s X’s turn to play (that is, the AI’s turn). And since there are three empty cells on the board, it implies that X has three possible play choices—top-middle, center, or bottom-right.
But which is the best choice? Which move will best help X minimize the maximum possibility of losing the game?
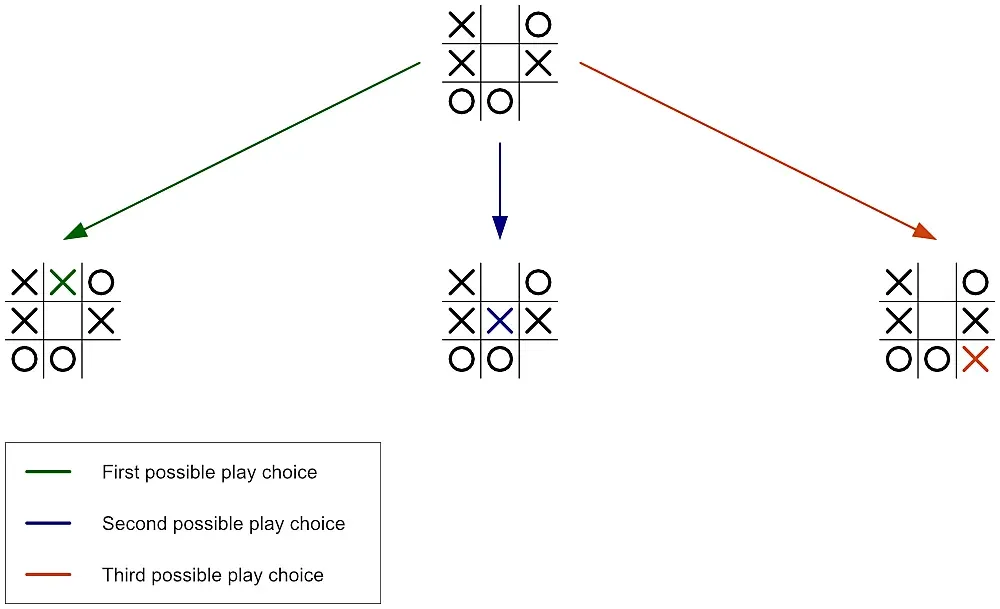
To make the best decision, AI needs to do the following:
- Store the current state (values) of the tic-tac-toe board in an array. (For any empty cell, the cell’s index will get stored as its present content).
- Get an array list of only the empty cells’ indexes.
- Check and confirm if a specific player has won the game.
- Recursively invoke minimax on each of the board’s empty cells.
- Return a score for every possible move of player X and player O.
- Out of all the returned scores, choose the best one (the highest) that is guaranteed to minimize the human player’s possibilities of winning the game.
We will configure the AI to accomplish the list above in the subsequent steps below. So, let’s get started by storing the board’s current state in an array.
Step 3: Store the Board’s Current State in an Array
Section titled “Step 3: Store the Board’s Current State in an Array”Our next step is to store the current content of each of the board’s cells in an array. So, replicate the snippet below inside step 2’s insertCompMark() function.
const currentBoardState = [];
gameCells.forEach((c, i) => { c.innerText ? currentBoardState.push(c.innerText) : currentBoardState.push(i);});In the snippet above, we:
- Created a
currentBoardStatearray - Stored the current value of each cell into the
currentBoardStatearray
Once the snippet above has completed its processing, the currentBoardState array would look like this:
["X", 1, "O", "X", 4, "X", "O", "O", 8];Step 4: Create a Function to Get the Indexes of All the Empty Cells
Section titled “Step 4: Create a Function to Get the Indexes of All the Empty Cells”The function below will:
- Receive the
currentBoardStatearray as its parameter’s argument. - Use JavaScript’s filter() method to create a new array containing all the
currentBoardStatearray’s items that are neither"X"nor"O".
function getAllEmptyCellsIndexes(currBdSt) { return currBdSt.filter((i) => i != "X" && i != "O");}Step 5: Create a Winner Determiner Function
Section titled “Step 5: Create a Winner Determiner Function”The primary purpose of the winner determiner function is to receive the currentBoardState array and a specific player’s mark (either mark "X" or "O") as its parameters’ arguments.
Then, it checks if the received mark forms a winning combination on the tic-tac-toe board. If so, the Boolean value true gets returned—otherwise, false gets returned.
function checkIfWinnerFound(currBdSt, currMark) { if ( (currBdSt[0] === currMark && currBdSt[1] === currMark && currBdSt[2] === currMark) || (currBdSt[3] === currMark && currBdSt[4] === currMark && currBdSt[5] === currMark) || (currBdSt[6] === currMark && currBdSt[7] === currMark && currBdSt[8] === currMark) || (currBdSt[0] === currMark && currBdSt[3] === currMark && currBdSt[6] === currMark) || (currBdSt[1] === currMark && currBdSt[4] === currMark && currBdSt[7] === currMark) || (currBdSt[2] === currMark && currBdSt[5] === currMark && currBdSt[8] === currMark) || (currBdSt[0] === currMark && currBdSt[4] === currMark && currBdSt[8] === currMark) || (currBdSt[2] === currMark && currBdSt[4] === currMark && currBdSt[6] === currMark) ) { return true; } else { return false; }}Step 6: Create the Minimax Algorithm
Section titled “Step 6: Create the Minimax Algorithm”A minimax algorithm is just an ordinary function that contains statements to be executed once the function is invoked.
Therefore, the process of creating the algorithm is the same as creating any other function. So, let’s create one now.
function minimax(currBdSt, currMark) { // Space for the minimax's statements}That’s it! You’ve created a minimax function—albeit an empty one.
Our next step is to fill up the function with statements that the computer will execute once the function gets invoked. We will begin this process from step 8.
Step 7: First Minimax Invocation
Section titled “Step 7: First Minimax Invocation”To avoid any confusion later in this tutorial, let’s invoke our minimax function for the first time—while passing in the currentBoardState array and the aiMark as the function’s arguments.
const bestPlayInfo = minimax(currentBoardState, aiMark);Step 8: Store the Indexes of All Empty Cells
Section titled “Step 8: Store the Indexes of All Empty Cells”In this step, we will invoke the getAllEmptyCellsIndexes function that we created at step 4—while passing in the currentBoardState array as the function’s argument.
Then, we will store the returned array list of indexes inside a variable named availCellsIndexes.
const availCellsIndexes = getAllEmptyCellsIndexes(currBdSt);Step 9: Check If There Is a Terminal State
Section titled “Step 9: Check If There Is a Terminal State”At this stage, we need to verify if there is a terminal state on the tic-tac-toe board.
We will accomplish the verification by invoking the winner determiner function (created in step 5) for each player.
If the function finds a win state for the human player (the minimizer), it will return -1 (which signifies that the human player has won, and the AI has lost).
But if the function finds a win state for the AI player (the maximizer), it will return +1 (which indicates that the AI has won, and the human player has lost).
However, suppose the winner determiner function cannot find any empty cell on the board and if it can’t find any win state for either player. In that case, it will return 0 (zero)—which signifies that the game has ended in a tie.
Let’s now proceed to implement the terminal state verification by creating an if statement in our minimax() algorithm like so:
if (checkIfWinnerFound(currBdSt, humanMark)) { return { score: -1 };} else if (checkIfWinnerFound(currBdSt, aiMark)) { return { score: 1 };} else if (availCellsIndexes.length === 0) { return { score: 0 };}The snippet above tells the active minimax function to return the appropriate terminal state score (-1, +1, or 0) and end its invocation whenever it finds a terminal state (lose, win, or draw).
Keep in mind that suppose the active minimax ends its invocation here. In such a case, the algorithm will move on to step 12.
However, suppose there is no terminal state. In that case, the active minimax function will execute the next statement (step 10, below).
Step 10: Get Ready to Test the Outcome of Playing the Current Player’s Mark on Each Empty Cell
Section titled “Step 10: Get Ready to Test the Outcome of Playing the Current Player’s Mark on Each Empty Cell”As step 9 found no terminal state, we have to devise a way to test what will happen if the current player (who is to make the next game move) plays on each empty cell.
In other words, if the current player plays on the first available cell, and the opponent plays on the second empty cell, will the current player win, lose, or draw the game? Or will there still be no terminal state found?
Alternatively, what will happen if the current player plays on the second available cell and the opponent plays on the first empty cell?
Or perhaps, will the third available cell be the best spot for the current player to play?
This test drive is what we need to do now. But before we begin, we need a place to record each test’s outcome—so let’s do that first by creating an array named allTestPlayInfos.
const allTestPlayInfos = [];So, now that we have secured a place to store each test drive’s result, let’s begin the trials by creating a for-loop statement that will loop through each of the empty cells starting from the first one.
for (let i = 0; i < availCellsIndexes.length; i++) { // Space for the for-loop's codes}In the next two steps, we will fill up the for-loop with the codes it should run for each empty cell.
Step 11: Test-Play the Current Player’s Mark on the Empty Cell the For-Loop Is Currently Processing
Section titled “Step 11: Test-Play the Current Player’s Mark on the Empty Cell the For-Loop Is Currently Processing”Before doing anything in this step, let’s review the current state of our board.
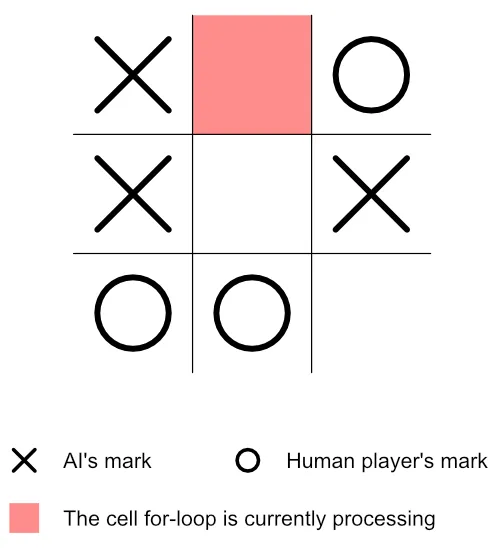
Notice that the gameboard above is still the same as that of figure 2, except that we’ve highlighted—in red—the cell the for-loop is currently processing.
Next, it will be helpful to have a place to store this test-play’s terminal score—so let’s create an object in the for-loop like so:
const currentTestPlayInfo = {};Also, before test-playing the current player’s mark on the red cell, let’s save the cell’s index number—so that it will be easy to reset the cell’s info after this test-play.
currentTestPlayInfo.index = currBdSt[availCellsIndexes[i]];Let’s now place the current player’s mark on the red cell (that is, the cell currently being processed by the for-loop).
currBdSt[availCellsIndexes[i]] = currMark;Based on the current player’s gameplay, the board’s state will change to reflect the latest move.
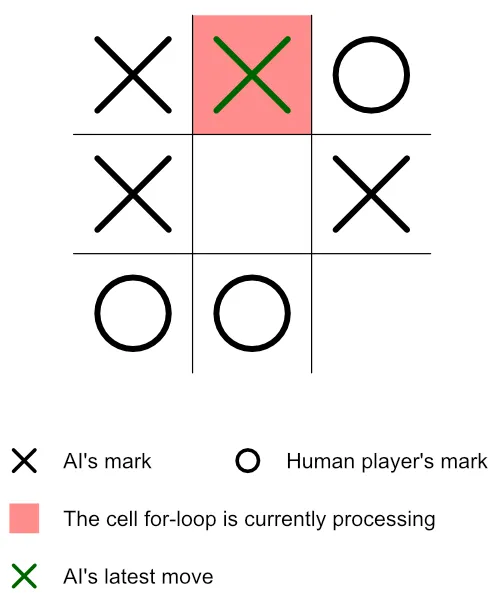
Figure 5: The new board—which reflects the current player’s latest move
Therefore, since the board’s state has changed, we need to recursively run minimax on the new board—while passing in the new board’s state and the next player’s mark.
if (currMark === aiMark) { const result = minimax(currBdSt, humanMark);} else { const result = minimax(currBdSt, aiMark);}Step 12: Save the Latest Terminal Score
Section titled “Step 12: Save the Latest Terminal Score”After the just concluded minimax invocation has returned its terminal state’s value, the active for-loop will save the result variable’s score into the currentTestPlayInfo object in the following way:
currentTestPlayInfo.score = result.score;Therefore, update step 11’s if statement like so:
if (currMark === aiMark) { const result = minimax(currBdSt, humanMark); currentTestPlayInfo.score = result.score;} else { const result = minimax(currBdSt, aiMark); currentTestPlayInfo.score = result.score;}Then, since the returned score officially ends the current test-play, it is best to reset the current board back to the state before the current player made its move.
currBdSt[availCellsIndexes[i]] = currentTestPlayInfo.index;Also, we need to save the result of the current player’s test-play for future use. So, let’s do that by pushing the currentTestPlayInfo object to the allTestPlayInfos array like so:
allTestPlayInfos.push(currentTestPlayInfo);Step 13: Run the Active For-Loop on the Next Empty Cell
Section titled “Step 13: Run the Active For-Loop on the Next Empty Cell”Remember that the currently active for-loop (that began at step 10) has only finished its work for the preceding empty cell(s). Therefore, the loop will proceed to test-play the current player’s mark on the next free cell.
In other words, the currently running minimax function will repeat steps 11 and 12. But, essentially, take note of the following:
- The red cell highlighted in figure 4 will change to the cell the for-loop is currently processing.
- Please, be mindful that figure 5 will also change. In other words, the current player’s move will now be on the cell the for-loop is currently processing.
- After the active for-loop has completed its work, the
allTestPlayInfosarray will contain specific objects for each empty cell the for-loop has processed. - Each of the objects in the
allTestPlayInfosarray will contain anindexproperty and ascoreproperty (take for example:{ index: 8, score: -1 }). - If you got to this step from step 20, then, on completing step 12, kindly continue this tutorial at step 18.
Step 14: Plan How to Get the Object with the Best Test-Play Score for the Current Player
Section titled “Step 14: Plan How to Get the Object with the Best Test-Play Score for the Current Player”Immediately after the for-loop has completed its work of looping through all the empty cells of the current board, minimax will:
- Create a space to store the reference number that will later help to get the best test-play object.
- Get the reference number to the current player’s best test-play.
- Use the acquired reference number to get the object with the best test-play for the current player.
Let’s implement this plan in the next few steps.
Step 15: Create a Store for the Best Test-Play’s Reference
Section titled “Step 15: Create a Store for the Best Test-Play’s Reference”The variable below is where we will later store the reference to the best test-play object. Place it immediately after the for-loop.
let bestTestPlay = null;Step 16: Get the Reference to the Current Player’s Best Test-Play
Section titled “Step 16: Get the Reference to the Current Player’s Best Test-Play”Now that there is a bestTestPlay store, the active minimax function can proceed to get the reference to the current player’s best test-play like so:
if (currMark === aiMark) { let bestScore = -Infinity; for (let i = 0; i < allTestPlayInfos.length; i++) { if (allTestPlayInfos[i].score > bestScore) { bestScore = allTestPlayInfos[i].score; bestTestPlay = i; } }} else { let bestScore = Infinity; for (let i = 0; i < allTestPlayInfos.length; i++) { if (allTestPlayInfos[i].score < bestScore) { bestScore = allTestPlayInfos[i].score; bestTestPlay = i; } }}The code above means if the current mark is equal to the AI player’s mark:
- Create a
bestScorevariable with the value of-Infinity. (Note that this value is just a placeholder value that needs to be less than all the scores in theallTestPlayInfosarray. Therefore, using-700will do the same job). - Then, for every test-play object in the
allTestPlayInfosarray, check if the test-play the loop is currently processing has a higher score than the currentbestScore. If so, record that test-play’s details inside thebestScoreand thebestTestPlayvariables.
Otherwise, if the current mark is the human player’s mark:
- Create a
bestScorevariable with the value of+Infinity. (Again, note that we would get the same outcome if we had preferred to use+300. The value is just a placeholder value that needs to be greater than all the scores in theallTestPlayInfosarray). - Then, for every test-play object in the
allTestPlayInfosarray, check if the test-play the loop is currently processing has a lesser score than the currentbestScore. If so, save that test-play’s details inside thebestScoreand thebestTestPlayvariables.
Step 17: Get the Object with the Best Test-Play Score for the Current Player
Section titled “Step 17: Get the Object with the Best Test-Play Score for the Current Player”Finally, the currently running minimax invocation can now finish its work by returning the object with the best test-play for the current player like so:
return allTestPlayInfos[bestTestPlay];Note that minimax will store the returned object inside the result variable of the first for-loop that began at step 11. It will then repeat step 12. (Please revisit step 12 only. Then, continue this tutorial below.)
Step 18: Let’s Do a Review
Section titled “Step 18: Let’s Do a Review”This stage is an excellent time to review what we’ve done thus far pictorially.
Step 19: Tracing Our Steps with a Diagram
Section titled “Step 19: Tracing Our Steps with a Diagram”The diagram below shows the AI and the human player’s first test-play for the first for-loop invocation initiated by the AI player.
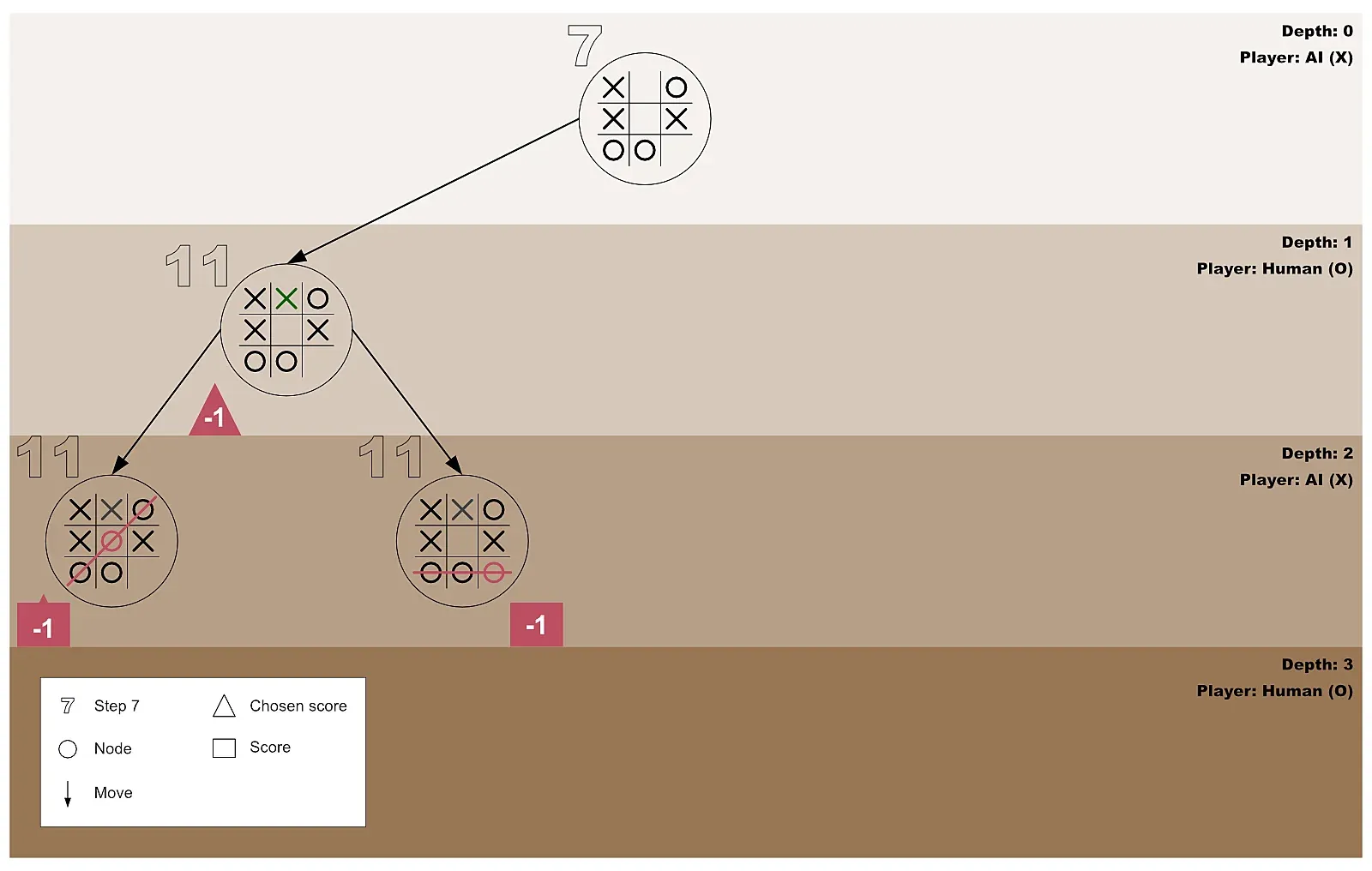
Figure 6: First test-play which predicts a loss state for the AI (maximizer)
Step 20: The First For-Loop Moves Forward to Process the Next Empty Cell
Section titled “Step 20: The First For-Loop Moves Forward to Process the Next Empty Cell”On concluding that playing on the first empty cell will end in a loss state, the AI forges ahead to test the outcome of playing on the second free cell by repeating step 13.
Step 21: Tracing Our Steps with a Diagram
Section titled “Step 21: Tracing Our Steps with a Diagram”The diagram below shows the AI and the human player’s second test-play for the first for-loop invocation initiated by the AI player.
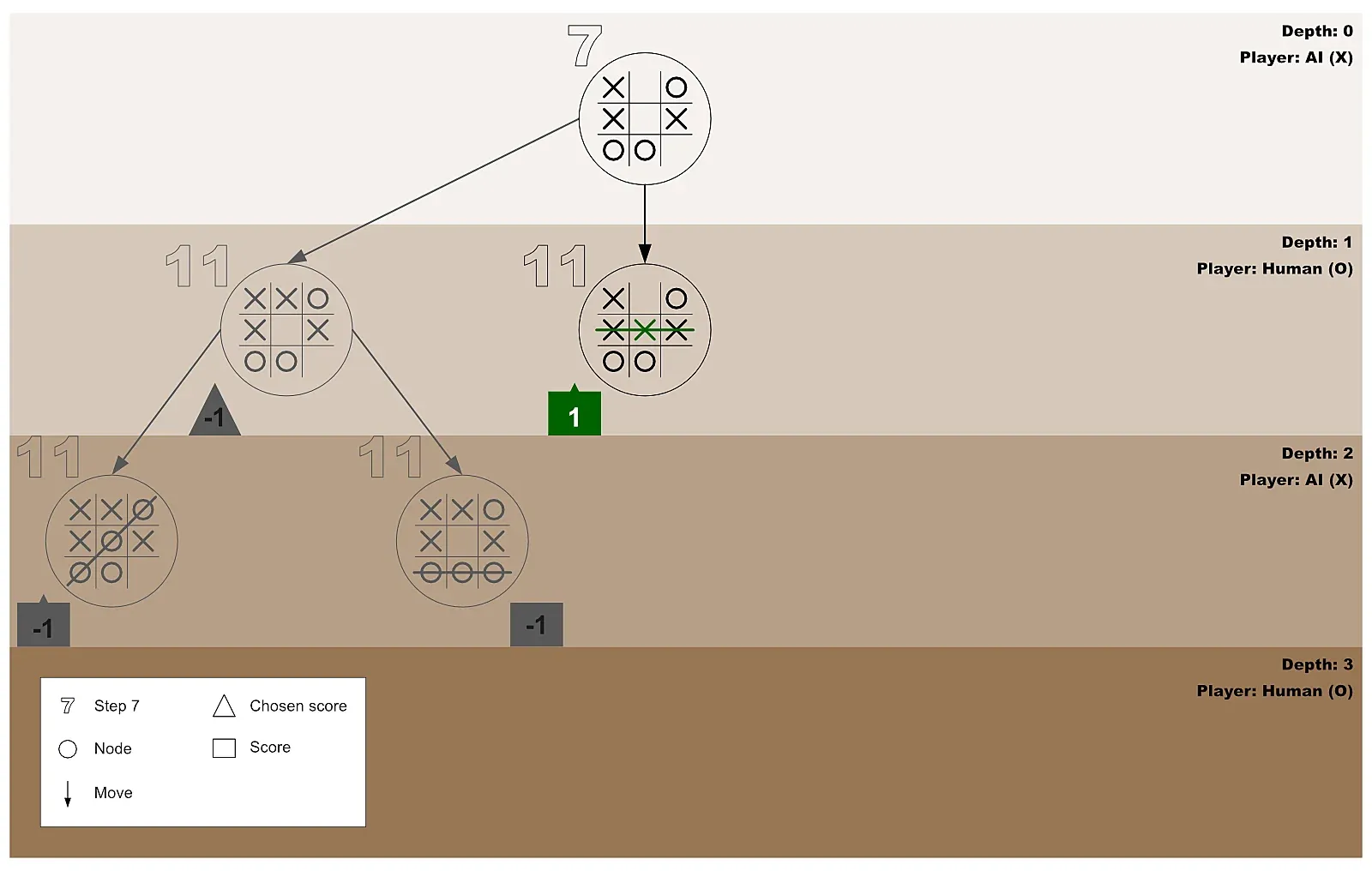
Figure 7: Second test-play which predicts a win state for the AI (maximizer)
Step 22: The First For-Loop Moves Forward to Process the Next Empty Cell
Section titled “Step 22: The First For-Loop Moves Forward to Process the Next Empty Cell”Now that the AI has confirmed that playing on the second empty cell will result in a win state, it further checks the outcome of playing on the third free cell by repeating step 13.
Step 23: Tracing Our Steps with a Diagram
Section titled “Step 23: Tracing Our Steps with a Diagram”The diagram below shows the AI and the human player’s third test-play for the first for-loop invocation initiated by the AI player.
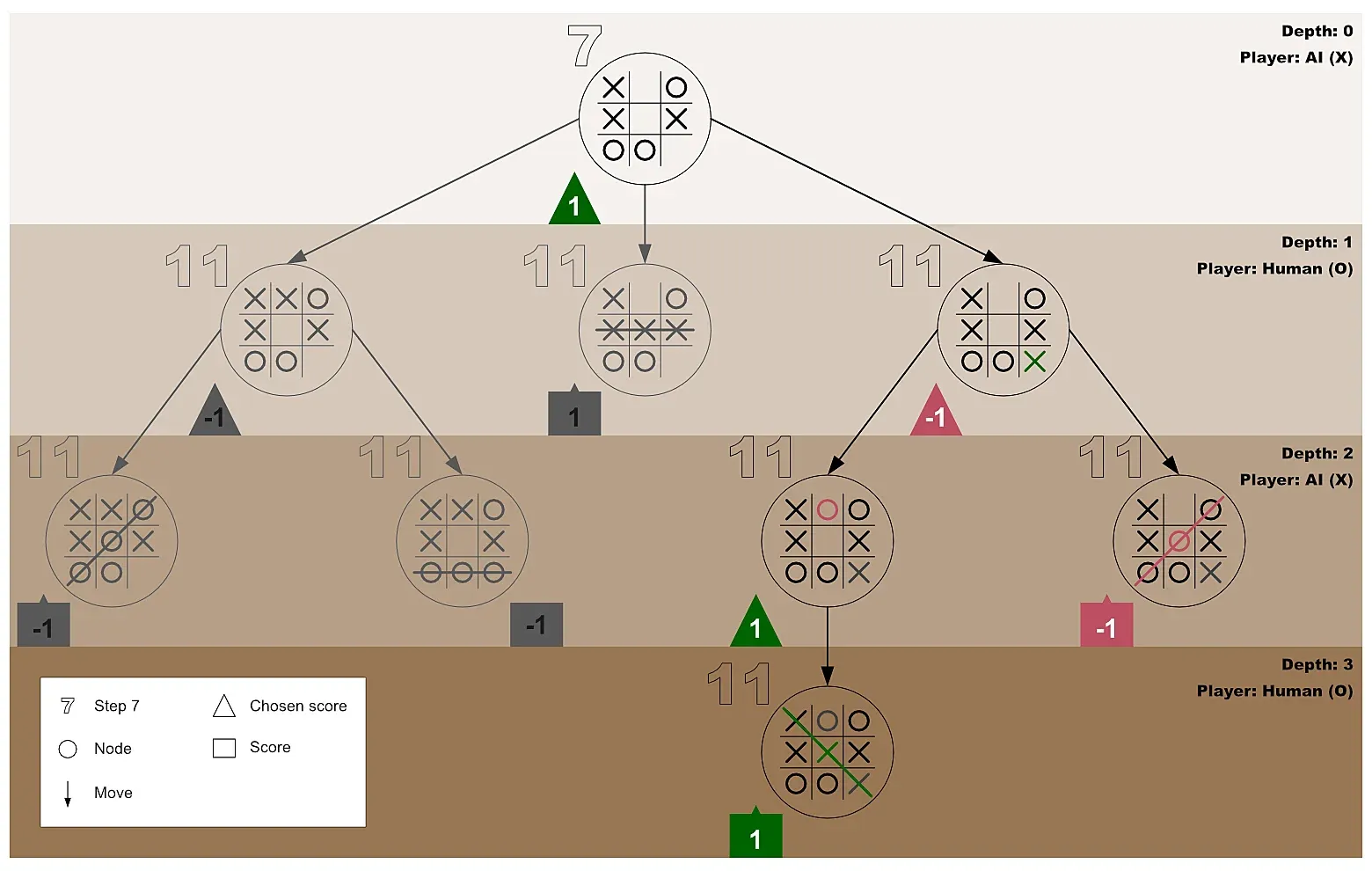
Figure 8: Third test-play which predicts a loss state for the AI (maximizer)
Step 24: Get the Object with the Best Test-Play Score for the AI Player
Section titled “Step 24: Get the Object with the Best Test-Play Score for the AI Player”At this point (after the third test-play), the first for-loop would have processed all the three empty cells of the first board (passed-in to minimax at step 7).
Therefore, minimax will forge ahead to get the object with the best test-play for the AI player—by repeating steps 15 to 17. However, when at step 17, kindly note the following:
- The returned object will now get stored in the
bestPlayInfovariable that we created at step 7. - Minimax will not repeat step 12 because the for-loop statement is no longer active.
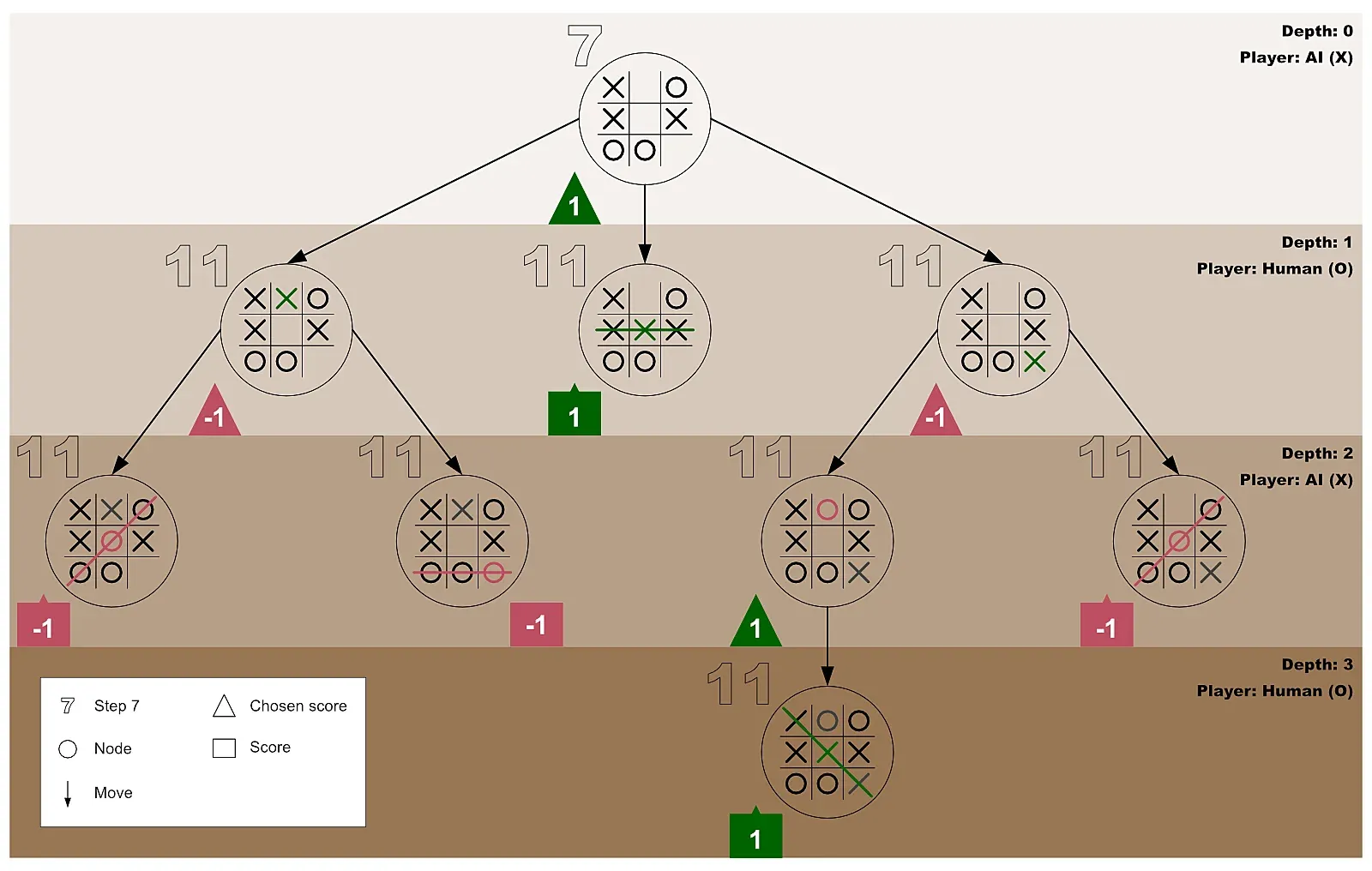
Step 25: Play on the Favorable Cell
Section titled “Step 25: Play on the Favorable Cell”Considering this tutorial’s board (a near-the-end state game board—as shown in figure 2 of step 1), the object in step 7’s bestPlayInfo variable will be { index: 4, score: 1 }.
Therefore, the AI can now use bestPlayInfo’s index value to choose the best cell to play on. So, place the following code after step 7’s bestPlayInfo variable.
gameCells[bestPlayInfo.index].innerText = aiMark;Step 26: Check If the Game Is Over
Section titled “Step 26: Check If the Game Is Over”After the AI has played, the next step is to check if the game is over.
In other words, after each player’s move, the next step is to verify:
- If the game has ended in a win state for the latest player
- If the game has ended in a draw for both players
- Or, if the game has not ended
So, update step 2’s checkIfGameIsOver() function with the code that will help implement the game-over verification.
function checkIfGameIsOver() { const rowsColsAndDiagsKeys = [ "rowOne", "rowTwo", "rowThree", "columnOne", "columnTwo", "columnThree", "diagonalOne", "diagonalTwo", ];
const rowsColsAndDiags = { rowOne: document.querySelectorAll(".r1"), rowTwo: document.querySelectorAll(".r2"), rowThree: document.querySelectorAll(".r3"), columnOne: document.querySelectorAll(".c1"), columnTwo: document.querySelectorAll(".c2"), columnThree: document.querySelectorAll(".c3"), diagonalOne: document.querySelectorAll(".d1"), diagonalTwo: document.querySelectorAll(".d2"), };
const cellValuesKeys = [ "rowOneCellsValues", "rowTwoCellsValues", "rowThreeCellsValues", "columnOneCellsValues", "columnTwoCellsValues", "columnThreeCellsValues", "diagonalOneCellsValues", "diagonalTwoCellsValues", ];
const cellValues = { rowOneCellsValues: [], rowTwoCellsValues: [], rowThreeCellsValues: [], columnOneCellsValues: [], columnTwoCellsValues: [], columnThreeCellsValues: [], diagonalOneCellsValues: [], diagonalTwoCellsValues: [], };
// Push each row, column, and diagonal cells' values into the appropriate array of the cellValues object: for (let i = 0; i < rowsColsAndDiagsKeys.length; i++) { rowsColsAndDiags[rowsColsAndDiagsKeys[i]].forEach((c) => cellValues[cellValuesKeys[i]].push(c.innerText) ); }
// Change the font color of the row, column, or diagonal cells whose values form a winning combination to color green: for (let i = 0; i < cellValuesKeys.length; i++) { if ( cellValues[cellValuesKeys[i]].every( (v) => v === cellValues[cellValuesKeys[i]][0] && v !== "" ) ) { gameOver = true; rowsColsAndDiags[rowsColsAndDiagsKeys[i]].forEach( (c) => (c.style.color = "green") ); } }
// If all cells have a value ("X" or "O"), and gameOver is still "false", change the gameOver variable to "true" and change all cells' font color to grey to reflect that the game is a draw: if (Array.from(gameCells).every((i) => i.innerText) && !gameOver) { gameOver = true; gameCells.forEach((i) => (i.style.color = "grey")); }}Since the game-over verification occurred after AI’s gameplay at step 25, the snippet above would confirm that the game has ended in a win state for the AI.
Therefore, the new board will look like so:
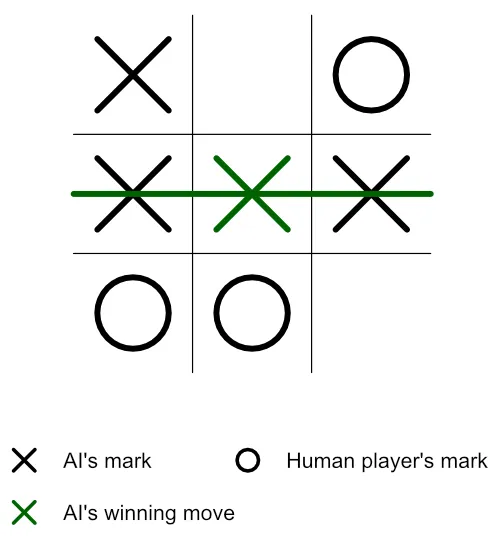
Figure 10: Final gameboard showing that the AI (player X) has won the game
Step 27: A Bird’s-Eye View of This Tutorial’s Algorithm
Section titled “Step 27: A Bird’s-Eye View of This Tutorial’s Algorithm”Below is this tutorial’s minimax algorithm in one piece.
Feel free to insert it into your editor and play around with it for various game scenarios until you are comfortable building an unbeatable AI! You can also see mine.
// Step 2 - Add some logic:const playGameBtn = document.getElementById("play-game-btn");const newGameBtn = document.getElementById("new-game-btn");const gameCells = document.querySelectorAll(".cell");const aiMark = "X";const humanMark = "O";
let gameOver = true;
gameCells.forEach((c) => c.addEventListener("click", insertPlayersMark));playGameBtn.addEventListener("click", playGame);newGameBtn.addEventListener("click", startNewGame);
function insertPlayersMark() { if (!this.innerText && !gameOver) { this.innerText = humanMark; checkIfGameIsOver(); } if (!gameOver) { insertCompMark(); checkIfGameIsOver(); }}
function playGame() { insertCompMark(); checkIfGameIsOver(); playGameBtn.style.display = "none"; newGameBtn.style.display = "block";}
function startNewGame() { gameOver = false; gameCells.forEach((i) => { i.innerText = ""; i.style.color = "#4b3621"; });}
function insertCompMark() { // Step 3 - Store the board's current state in an array: const currentBoardState = [];
gameCells.forEach((c, i) => { c.innerText ? currentBoardState.push(c.innerText) : currentBoardState.push(i); });
// Step 4 - Create a function to get the indexes of all the empty cells: function getAllEmptyCellsIndexes(currBdSt) { return currBdSt.filter((i) => i != "X" && i != "O"); }
// Step 5 - Create a winner determiner function: function checkIfWinnerFound(currBdSt, currMark) { if ( (currBdSt[0] === currMark && currBdSt[1] === currMark && currBdSt[2] === currMark) || (currBdSt[3] === currMark && currBdSt[4] === currMark && currBdSt[5] === currMark) || (currBdSt[6] === currMark && currBdSt[7] === currMark && currBdSt[8] === currMark) || (currBdSt[0] === currMark && currBdSt[3] === currMark && currBdSt[6] === currMark) || (currBdSt[1] === currMark && currBdSt[4] === currMark && currBdSt[7] === currMark) || (currBdSt[2] === currMark && currBdSt[5] === currMark && currBdSt[8] === currMark) || (currBdSt[0] === currMark && currBdSt[4] === currMark && currBdSt[8] === currMark) || (currBdSt[2] === currMark && currBdSt[4] === currMark && currBdSt[6] === currMark) ) { return true; } else { return false; } }
// Step 6 - Create the minimax algorithm: function minimax(currBdSt, currMark) { // Step 8 - Store the indexes of all empty cells: const availCellsIndexes = getAllEmptyCellsIndexes(currBdSt);
// Step 9 - Check if there is a terminal state: if (checkIfWinnerFound(currBdSt, humanMark)) { return { score: -1 }; } else if (checkIfWinnerFound(currBdSt, aiMark)) { return { score: 1 }; } else if (availCellsIndexes.length === 0) { return { score: 0 }; }
// Step 10 - Create a place to record the outcome of each test play: const allTestPlayInfos = [];
// Step 10 - Create a for-loop statement that will loop through each of the empty cells: for (let i = 0; i < availCellsIndexes.length; i++) { // Step 11 - Create a place to store this test-play's terminal score: const currentTestPlayInfo = {};
// Step 11 - Save the index number of the cell this for-loop is currently processing: currentTestPlayInfo.index = currBdSt[availCellsIndexes[i]];
// Step 11 - Place the current player's mark on the cell for-loop is currently processing: currBdSt[availCellsIndexes[i]] = currMark;
if (currMark === aiMark) { // Step 11 - Recursively run the minimax function for the new board: const result = minimax(currBdSt, humanMark);
// Step 12 - Save the result variable's score into the currentTestPlayInfo object: currentTestPlayInfo.score = result.score; } else { // Step 11 - Recursively run the minimax function for the new board: const result = minimax(currBdSt, aiMark);
// Step 12 - Save the result variable's score into the currentTestPlayInfo object: currentTestPlayInfo.score = result.score; }
// Step 12 - Reset the current board back to the state it was before the current player made its move: currBdSt[availCellsIndexes[i]] = currentTestPlayInfo.index;
// Step 12 - Save the result of the current player's test-play for future use: allTestPlayInfos.push(currentTestPlayInfo); }
// Step 15 - Create a store for the best test-play's reference: let bestTestPlay = null;
// Step 16 - Get the reference to the current player's best test-play: if (currMark === aiMark) { let bestScore = -Infinity; for (let i = 0; i < allTestPlayInfos.length; i++) { if (allTestPlayInfos[i].score > bestScore) { bestScore = allTestPlayInfos[i].score; bestTestPlay = i; } } } else { let bestScore = Infinity; for (let i = 0; i < allTestPlayInfos.length; i++) { if (allTestPlayInfos[i].score < bestScore) { bestScore = allTestPlayInfos[i].score; bestTestPlay = i; } } }
// Step 17 - Get the object with the best test-play score for the current player: return allTestPlayInfos[bestTestPlay]; }
// Step 7 - First minimax invocation: const bestPlayInfo = minimax(currentBoardState, aiMark);
// Step 25 - Play on the favorable cell: gameCells[bestPlayInfo.index].innerText = aiMark;}
// Step 26 - Check if the game is over:function checkIfGameIsOver() { const rowsColsAndDiagsKeys = [ "rowOne", "rowTwo", "rowThree", "columnOne", "columnTwo", "columnThree", "diagonalOne", "diagonalTwo", ];
const rowsColsAndDiags = { rowOne: document.querySelectorAll(".r1"), rowTwo: document.querySelectorAll(".r2"), rowThree: document.querySelectorAll(".r3"), columnOne: document.querySelectorAll(".c1"), columnTwo: document.querySelectorAll(".c2"), columnThree: document.querySelectorAll(".c3"), diagonalOne: document.querySelectorAll(".d1"), diagonalTwo: document.querySelectorAll(".d2"), };
const cellValuesKeys = [ "rowOneCellsValues", "rowTwoCellsValues", "rowThreeCellsValues", "columnOneCellsValues", "columnTwoCellsValues", "columnThreeCellsValues", "diagonalOneCellsValues", "diagonalTwoCellsValues", ];
const cellValues = { rowOneCellsValues: [], rowTwoCellsValues: [], rowThreeCellsValues: [], columnOneCellsValues: [], columnTwoCellsValues: [], columnThreeCellsValues: [], diagonalOneCellsValues: [], diagonalTwoCellsValues: [], };
// Push each row, column, and diagonal cells' values into the appropriate array of the cellValues object: for (let i = 0; i < rowsColsAndDiagsKeys.length; i++) { rowsColsAndDiags[rowsColsAndDiagsKeys[i]].forEach((c) => cellValues[cellValuesKeys[i]].push(c.innerText) ); }
// Change the font color of the row, column, or diagonal cells whose values form a winning combination to color green: for (let i = 0; i < cellValuesKeys.length; i++) { if ( cellValues[cellValuesKeys[i]].every( (v) => v === cellValues[cellValuesKeys[i]][0] && v !== "" ) ) { gameOver = true; rowsColsAndDiags[rowsColsAndDiagsKeys[i]].forEach( (c) => (c.style.color = "green") ); } }
// If all cells have a value ("X" or "O"), and gameOver is still "false", change the gameOver variable to "true" and change all cells' font color to grey to reflect that the game is a draw: if (Array.from(gameCells).every((i) => i.innerText) && !gameOver) { gameOver = true; gameCells.forEach((i) => (i.style.color = "grey")); }}