CSS scaleZ() Function – How to Resize Elements along Z-axis

scaleZ() transforms an element by resizing (scaling) it three-dimensionally from a fixed point along the z-axis.

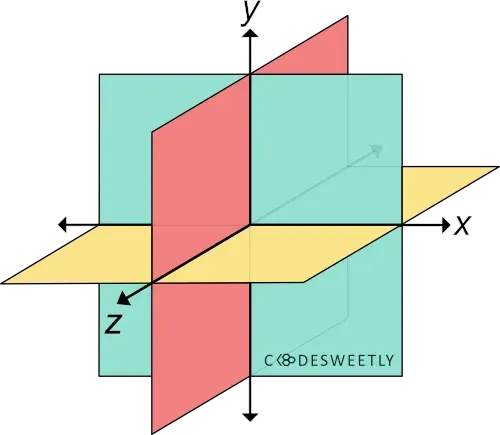
A three-dimensional Cartesian coordinate system showing the X-, Y-, and Z-axis

Note

• “Transform origin” is the fixed point from which the computer scales an element.
• You can define your element’s fixed point using the CSS transform-origin property. But the default is center.

Syntax of the CSS scaleZ() Function

scaleZ() accepts a single argument. Here is the syntax:

element {
  transform: scaleZ(number);
}

Note the following:

• The scaleZ(number) function is equivalent to scale3d(1, 1, number).
• The number argument specifies the element’s scaling factor along the z-axis.
• Whenever you include scaling or zooming animations in your app, provide users an option to turn off animations. This option is necessary because scaling and zooming animations cause accessibility issues.

Examples of the CSS scaleZ() Function

We often use scaleZ() with other CSS functions such as perspective(), translateZ(), and rotateX(). Below are some examples.

How to use scaleZ() with CSS perspective() and rotateX() functions

CSS

img {
  transform: perspective(370px) scaleZ(5) rotateX(17deg);
  width: 80%;
}

HTML

<img
  src="https://cdn.pixabay.com/photo/2022/09/26/23/26/african-american-7481724_960_720.jpg"
  alt=""
/>

Try Editing It

Here’s what we did in the snippet above:

1. We used the perspective() function to define a 370px distance between the user and the z=0 plane.
2. The scaleZ() function specifies a scale factor of 5 for the image along the z-axis.
3. We used the rotateX() function to rotate the image seventeen-degree (17⁰) around the x-axis.

Note

• List perspective() first whenever you chain it with other CSS transform functions. Otherwise, browsers might transform the selected element incorrectly.
• List the scaleZ() function before rotateX(). Otherwise, the browser will not scale the element.

CodeSweetly ads

How to use scaleZ() with CSS perspective() and translateZ() functions

CSS

img {
  width: 40%;
}

.second-image {
  transform: perspective(370px) scaleZ(5) translateZ(30px);
}

HTML

<img
  class="first-image"
  src="https://cdn.pixabay.com/photo/2022/09/26/23/26/african-american-7481724_960_720.jpg"
  alt=""
/>

<img
  class="second-image"
  src="https://cdn.pixabay.com/photo/2022/09/26/23/26/african-american-7481724_960_720.jpg"
  alt=""
/>

Try Editing It

Here’s what we did in the snippet above:

1. We used the perspective() function to define a 370px distance between the user and the z=0 plane.
2. The scaleZ() function specifies a scale factor of 5 for the image along the z-axis.
3. We used the translateZ() function to reposition the second-image thirty pixels (30px) away from its original position along the z-axis.

Note

• List perspective() first whenever you chain it with other CSS transform functions. Otherwise, browsers might transform the selected element incorrectly.
• List the scaleZ() function before translateZ(). Otherwise, the browser will not scale the element.